libLCS - A Logic Circuit Simulation Library in C++

The aim of this example is the same as that of the example presented here. However, this time we will see how to create a functional realisation of a full-adder module, unlike a gate-level realisation as in that example. The circuit diagram is as follows.

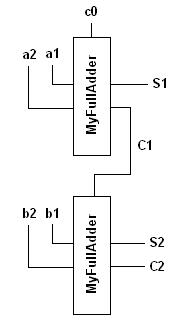
The code which implements the above circuit using functional modules of 1-bit full-adders is as follows. The implementation of the full-adder module here is the same as that of the full-adder class lcs::FullAdder provided in libLCS.

#include <lcs/or.h>
#include <lcs/and.h>
#include <lcs/not.h>
#include <lcs/tester.h>
#include <lcs/simul.h>
#include <lcs/changeMonitor.h>

// All classes of the libLCS are defined in the namespace lcs.
using namespace lcs;

using namespace std;

// Define a class MyFullAdder. The instances of this class will serve as
// 1-bit full-adder modules for our circuit.
class MyFullAdder : public Module
{
public:
    // The constructor should take single line Bus<1> objects as inputs, one each for
    // the two data lines, carry input, sum output and the carry output.
    MyFullAdder(const Bus<1> &S, const Bus<1> Cout, const InputBus<1> &A,
              const InputBus<1> &B, const InputBus<1> &Cin);

    // Destructor.
    //
    ~MyFullAdder();

    // This function is re-implemented from the class lcs::Module.
    // When state of any of the input bus lines changes, the corresponding bus
    // will call this function to notify the fulladder module of such a
    // change. This function then perform a 1-bit full binary addition of the
    // line states of input busses and propogate the result to the output busses.
    virtual void onStateChange(int portId);

private:
    Bus<1> s, cout;
    InputBus<1> a, b, c;
};

MyFullAdder::MyFullAdder(const Bus<1> &S, const Bus<1> Cout, const InputBus<1> &A,
                     const InputBus<1> &B, const InputBus<1> &Cin)
         : Module(), s(S), cout(Cout), a(A), b(B), c(Cin)
{
    // A functional module has to be driven by the data lines of the input busses.
    // In order to be driven, a module has to register itself with each of the input
    // busses using the drive function. If not registered, a change to the state of the data
    // lines of an input bus will not trigger the module to propogate the change and produce
    // the output.
    a.notify(this, LINE_STATE_CHANGE, 0);
    b.notify(this, LINE_STATE_CHANGE, 0);
    c.notify(this, LINE_STATE_CHANGE, 0);

    // An output bus which is driven by the full adder module should not simulataneously be driven
    // by another module. To avoid such a short-circuit, the output busses should be locked so
    // that only this module can drive them. If locked, an attempt to drive the bus by another module
    // will cause a lcs::ShortCircuitException to be thrown following a warning message. If not locked,
    // the same output bus can be driven simulatneously by two different anonymous modules leading to
    // undefined  behaviour, which will be hard to trace as neither a warning will be issued, nor an
    // exception will be thrown.
    s.lock(this);
    cout.lock(this);

    // After setting up the busses, the line data should be propogated to the output so that
    // the output is the one corresponding to the input after the module is constructed.
    onStateChange(0);
}

MyFullAdder::~MyFullAdder()
{
    // When a module ceases to exist anylonger, it should notify its input busses to stop triggering
    // it. This is done using the lcs::InputBus::stopNotification function. If not de-registered in this
    // way, the input busses will try to drive a non existant module, resulting in a segmentation fault.
    a.stopNotification(this, LINE_STATE_CHANGE, 0);
    b.stopNotification(this, LINE_STATE_CHANGE, 0);
    c.stopNotification(this, LINE_STATE_CHANGE, 0);

    // The output busses should be un-locked by this module so that they can be driven by other modules.
    s.unLock(this);
    cout.unLock(this);
}

void MyFullAdder::onStateChange(int portId)
{
    // The sum and carry outputs are calculated using the overloaded bitwise operators
    // rather than through an ensemble of logics gates.
    LineState sum = (!a[0] & !b[0] & c[0]) | (!a[0] & b[0] & !c[0]) |
                    (a[0] & !b[0] & !c[0]) | (a[0] & b[0] & c[0]) ,
              carry = (!a[0] & b[0] & c[0]) | (a[0] & !b[0] & c[0]) |
                      (a[0] & b[0] & !c[0]) | (a[0] & b[0] & c[0]) ;

    // The corresponding LineAccessor objects should be used to set the lines of the
    // output busses.
    Bus<>::LineAccessor sumLines(s.getLineAccessor(this)),
                        carryLines(cout.getLineAccessor(this));

    // The LineAccessor objects come with an overloaded operator[] for convenience.
    sumLines[0] = sum;
    carryLines[0] = carry;
}

int main(void)
{
    // Declaring the busses involved in out circuit.
    // Note that the bus c0 (the carry input to the first full-adder)
    // has been initialised with a value of 0 (or lcs::LOW) on its line.
    Bus<> a1, b1, a2, b2, c0(0), S1, C1, S2, C2;

    // Initialising the 1-bit full adder modules.
    MyFullAdder fa1(S1, C1, a1, a2, c0), fa2(S2, C2, b1, b2, C1);

    // Initialising lcs::ChangeMonitor objects which monitor the inputs and the
    // 3 sum bits.
    ChangeMonitor<4> inputMonitor((a1,b1,a2,b2), "Input");
    ChangeMonitor<3> outputMonitor((S1,S2,C2), "Sum");

    Tester<4> tester((a1,b1,a2,b2));

    Simulation::setStopTime(2000); // Set the time upto which the simulation should run.
    Simulation::start();           // Start the simulation.


    return 0;
}

- A Logic Circuit Simulation Library in C++

(libLCS Example) Functional module of a 1-bit fulladder